1. Persegi

Persegi merupakan sebuah bangun datar yang memiliki 4 sisi yang panjang tiap sisinya sama panjang, selain itu bangun datar persegi memiliki 4 sudut siku-siku yang sama besar yaitu 900.
Kita dapat menemukan bangun datar yang berbentuk persegi dalam kehidupan sehari-hari, diantaranya : keramik lantai, ubin lantai, dan lain-lain.
Rumus Luas Persegi = sisi x sisi
Rumus Keliling Persegi = 4 x sisi
SOAL :
Berikut contoh soal dan pembahasan bangun datar persegi :
Sebuah persegi memiliki sisi 5 cm, tentukan luas dan keliling bangun tersebut !
 |
Pembahasan :
a. Luas persegi ABCD = s x s
= 5 cm x 5 cm
= 25 cm2.
Jadi, luas persegi ABCD adalah 25 cm2.
b. Keliling persegi ABCD = 4 x s
= 4 x 5 cm
= 20 cm.
Jadi, keliling persegi ABCD adalah 20 cm.
2. Persegi Panjang

Persegi Panjang merupakan sebuah bangun datar yang memiliki 2 sisi lebar yang besarnya sama dan 2 sisi panjang yang besarnya sama. Keempat sudut nya sama besar masing-masing memiliki besar 900.
Kita dapat menemukan bangun datar yang berbentuk persegi panjang dalam kehidupan sehari hari, diantaranya :
lapangan bulutangkis, plavon atap, buku gambar, dan lain-lain.
Panjang (P) dan Lebar (l)
Rumus Luas Persegi Panjang = P x l
Rumus Keliling Persegi Panjang = 2 x (P+l)
SOAL :
Berikut contoh soal dan pembahasan bangun datar persegi panjang :
Sebuah persegi panjang EFGH, memiliki lebar 5 cm dan panjang 10 cm, tentukan,
a. Luas Persegi panjang EFGH
b. Keliling Persegi panjang EFGH
 |
| . |
Pertanyaan :
a. Tentukan luas persegi panjang EFGH!
b. Tentukan keliling persegi panjang EFGH!
Pembahasan :
a. Luas persegi panjang EFGH = p x l
= 10 cm x 5 cm
= 50 cm2.
Jadi, luas persegi panjang EFGH adalah 50 cm2.
b. Keliling persegi panjang EFGH = 2 x (p + l)
= 2 x (10 cm + 5 cm)
= 2 x 15 cm.
= 30 cm
Jadi, keliling persegi panjang EFGH adalah 30 cm.
3. Segitiga

Segitiga merupakan salah satu bangun datar yang mempunyai 3 sisi. bangun datar ini ada 3 macam, diantaranya segitiga sama sisi, segitiga siku – siku, dan segitiga sembarang.
Bangun datar segitiga mempunyai rumus luas dan keliling sebagai berikut;
Luas = ½ x a x t
Keliling = Sisi + Sisi + Sisi
= a + b + c
Berikut contoh soal dan pembahasan bangun datar Segitiga:
SOAL :
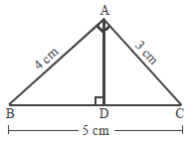
Sebuah bangun datar segitiga BAC, dengan siku-siku di A memiliki panjang sisi AB = 4cm, BC = 5cm dan
AC = 3cm
Pertanyaan :
a. Tentukan luas segitiga BAC !
b. Tentukan keliling segitiga BAC !
Pembahasan :
a. Luas segitiga BAC = ½ x a x t
= ½ x 3 cm x 4 cm
= 6 cm
Jadi, luas segitiga BAC adalah 6 cm2.
Catatan:
- Dalam menentukan tinggi dan alas segitiga adalah : tinggi segitiga merupakan sisi tegak yang harus tegak lurus dengan alasnya (jadi bisa dikatakan bahwa pertemuan antara alas dan tinggi segitiga akan membentuk sudut siku-siku
b. Keliling segitiga BAC = Sisi AB + Sisi BC + Sisi CA
= 4 cm + 5 cm + 3 cm
= 12 cm
4. Belah Ketupat
4. Belah Ketupat
Belah Ketupat merupakan salah satu bangun datar yang memiliki 4 sisi. ke-empat sisi bangun datar ini sama panjang, tetapi ke-empat sudutnya tidak siku-siku. Sehingga bangun datar ini memiliki 2 diagonal (d) yang kedua diagonalnya tidak sama panjang.
Kita dapat menemukan barang-barang yang bentuknya seperti bangun datar ini dalam kehidupan sehari-hari. Diantaranya : gantungan permata, ketupat,dll
Bangun datar Belah Ketupat mempunyai rumus luas dan keliling sebagai berikut;
Luas = ½ x d1 x d2
Keliling = Sisi + Sisi +Sisi + Sisi
= 4 x Sisi
Berikut contoh soal dan pembahasan bangun datar Belah Ketupat:
SOAL :
Sebuah bangun datar belah ketupat ABCD mempunyai sisi dengan panjang 10 cm, dan mempunyai 2 diagonal AC dan BD. Tentukan Luas dan Keliling belah ketupat tersebut.
Pembahasan :
*Panjang Diagonal AC = 12 cm..............(d1)
*Panjang Diagonal BD = 16 cm..............(d2)
a. Luas Belah Ketupat = ½ x d1 x d2
= ½ x 12 x 16
= 96 cm2
Jadi, luas Belah Ketupat ABCD adalah 96 cm2.
b. Keliling Belah Ketupat = 4 x Sisi
= 4 x 10 cm
= 40 cm
Jadi, keliling Belah Ketupat ABCD adalah 40 cm.
5. Jajar Genjang
Jajar genjang merupakan bangun datar yang memiliki 2 pasang sisi yang saling sejajar, namun sisi sisi yang berhimpit tidak membentuk sudut siku-siku.
Bangun datar Jajar Genjang mempunyai rumus luas dan keliling sebagai berikut;
Luas = alas x tinggi
= a x t
= 2 (alas + sisi miring)
= 2a + 2b
SOAL :
Sebuah bangun datar jajar genjang ABCD mempunyai tinggi 7 Cm, panjang sisi AB=DC=AD=BC=8Cm
Pertanyaan:
a. Tentukan luas jajaran genjang ABCD!
b. Tentukan keliling jajaran genjang ABCD!
Pembahasan:
a. Luas jajaran genjang ABCD = a x t
= 8 cm x 7 cm
= 56 cm2
Jadi, luas jajaran genjang ABCD adalah 56 cm2.
b. Keliling jajaran genjang ABCD = s + s + s + s
= AB + BC + CD + DA
= 8 cm + 8 cm + 8 cm + 8 cm
= 32 cm.
Jadi, keliling jajaran genjang ABCD adalah 32 cm.
6. Layang-Layang
Layang layang merupakan bangun datar yang memiliki sepasang sisi yang sama panjang. Bangun datar ini juga mempunyai 2 diagonal yang saling berpotongan.
Dalam kehidupan sehari-hari kita bisa menemukan barang yang berbentuk layang-layang contohnya: mainan anak-anak layang-layang
Bangun datar layang-layang mempunyai rumus Luas dan Keliling sebagai berikut :
Luas = ½ x d1 x d2
Keliling = 2 x ( x+ y)
Berikut contoh soal dan pembahasan bangun datar Layang-layang :
SOAL :
Sebuah bangun datar layang-layang ABCD memiliki panjang sisi AB=AD=12 Cm, CB=CD=22 Cm, Panjang diagonal AC=30 Cm, Panjang diagonal BD=15 Cm.
Pertanyaan:
a. Tentukan Luas layang-layang ABCD
b. Tentukan Keliling layang-layang ABCD
Pembahasan:
a. Luas layang-layang ABCD = ½ x d1 x d2
= ½ x AC x BD
= ½ x 30 cm x 15 cm
= 225 cm2
Jadi, luas layang layang ABCD adalah 225 cm2.
b. Keliling layang layang ABCD = 2 x (x + y)
= 2 x (AB + BC)
= 2 x (12 cm + 22 cm)
= 2 x 34 cm
= 68 cm
Jadi, keliling layang layang ABCD adalah 68 cm.
7. Trapesium
Trapesium merupakan bangun datar yang memiliki 4 sisi, ada dua sisi yang sejajar. Bangun datar trapesium mempunyai rumus luas dan keliling sebagai berikut
Luas = ½ x Jumlah sisi sejajar x tinggi
= ½ x (a + c) x t
= a + b + c + d
Berikut contoh soal dan pembahasan bangun datar Trapesium :
SOAL :
Sebuah bangun datar trapesium EFGH, mempunyai panjang sisi EF= 16 cm, HG= 6 cm dan memiliki tinggi 7 cm
Pertanyaan:
a. Tentukan Luas trapesium EFGH
b. Tentukan Keliling trapesium EFGH
Pembahasan:
a. Luas trapesium EFGH = ½ x (a + b) x t
= ½ x (16 cm + 6 cm) x 7 cm
= ½ x 22 cm x 7 cm
= 11 cm x 7 cm
= 77 cm2
Jadi, luas trapesium EFGH adalah 77 cm2.
b. Keliling trapesium EFGH = s + s + s + s
= EF + FG + GH + HE
= 16 cm + 8 cm + 6 cm + 8 cm
= 38 cm.
Jadi, keliling trapesium EFGH adalah 38 cm.
8. Lingkaran
Lingkaran merupakan bangun datar yang bentuknya bulat dan tidak bersudut. Dalam kehidupan sehari-hari kita sering menemukan benda yang bentuk nyak lingkaran, seperti : kepingan mata uang logam, jam dinding, piring dll.
Bangun datar lingkaran mempunyai rumus luas dan keliling sebagai berikut
Luas = phi x jari-jari x jari-jari
= p
x
r2
Keliling = 2 x
p
x
r
=
p
d
Ket
Phi memiliki nilai 22/7 atau 3.14
r = jari-jari lingkaran
d = diameter lingkaran
d = 2 x r
SOAL :
Sebuah bangun datar Lingkaran, mempunyai diameter 14 cm
Pertanyaan:
a. Tentukan Luas lingkaran
b. Tentukan Keliling lingkaran
Pembahasan:
a. Luas lingkaran
= 22/7 x 7 cm x 7 cm
= 154 cm2
Jadi, luas lingkaran adalah 154 cm2.
b. Keliling lingkaran = π x d
= 22/7 x 14 cm
= 44 cm.
Jadi, keliling lingkaran adalah 44 cm.
b. Keliling lingkaran = π x d
= 22/7 x 14 cm
= 44 cm.
Jadi, keliling lingkaran adalah 44 cm.